FermCalc - Unit Conversion Calculator
- Introduction
- Calculation Details
- Specific Gravity / Density Conversions
- Specific Gravity <--> Brix
- Specific Gravity <--> Oechsle
- Specific Gravity <--> Baumé
- Specific Gravity <--> Klosterneuburger Mostwaage (KMW)
- Specific Gravity <--> Twaddell
- Specific Gravity <--> Density
- Specific Gravity <--> g/L Sugar
- Specific Gravity <--> Potential Alcohol
- Acidity Conversions
- Acid Reference
- Grams/Liter <--> Percent
- Grams/Liter <--> mEq/L
- Alcohol Content Conversions
- % Alcohol by Volume <--> % Alcohol by Weight
- % Alcohol by Volume <--> Proof (US)
- % Alcohol by Volume <--> Proof (British)
- Concentration Conversions
- Refractivity Conversions
- Refractive Index <--> Brix
- Refractive Index <--> Oechsle
- Refractive Index <--> Baumé
- Refractive Index <--> KMW
- Refractive Index <--> Zeiss Units
Introduction
The layout of the Conversions panel is somewhat similar to Josh Madison's excellent Convert program. Convert is freeware if you need a more comprehensive program for performing conversions.
FermCalc provides eight categories of unit conversions:
- Volume
- Mass
- Temperature
- Specific Gravity / Density
- Acidity
- Alcohol Content
- Concentration
- Refractivity
Calculation Details
Calculation details are provided below. Only the Specific Gravity, Acidity, Alcohol Content, Concentration, and Refractivity conversions are covered in detail here since the others are fairly straightforward. Unless otherwise stated below, the conversion factors are taken from F. Cardarelli (2003).
Back to topSpecific Gravity / Density Conversions
The specific gravity (SG) conversions are intended to convert between different hydrometer reading scales. The conversions to Brix, Oechsle, KMW, g/L sugar, and potential alcohol are only valid prior to fermentation. After fermentation begins these readings will be obscured by alcohol, and therefore reflect the apparent hydrometer readings for these quantities. All of these conversions assume a reference temperature of 20°C for SG.
Specific Gravity <--> Brix
Brix is equivalent to the sugar concentration in percent by weight in the juice or must. The Brix scale is virtually identical to the Balling and Plato scales. This is the most important conversion in FermCalc because it is used to calculate percent sugar by weight from SG in all of the sugar calculations. Calculating percent sugar from SG in this manner inherently assumes that there are no dissolved solids present in the must other than sugar. While this is never actually the case, since sugar calculations usually involve taking differences between initial and final specific gravities and sugar concentrations, this approximation usually yields acceptable results.
FermCalc uses the equation developed by J. Hackbarth (2011), which is based on the AOAC Brix tables (Horwitz and Latimer, 2005), to convert from Brix to SG. The equation is:
sg = 1 + Σk mk (B/100)k (1)
where
sg = specific gravity
B = degrees Brix
k = 1 to 10
m1 = +0.3875135555
m2 = +0.09702881653
m3 = +0.3883357480
m4 = -1.782845295
m5 = +5.591472292
m6 = -11.00667976
m7 = +13.62230734
m8 = -10.33082001
m9 = +4.387787019
m10 = -0.7995558730
FermCalc uses an iterative technique to solve equation (1) for B given a value of sg. For values of sg less than 1.0, the slope of the B vs. sg curve at sg = 1.0 is extrapolated to lower values to obtain the associated negative Brix values.
Previous versions of FermCalc used the sucrose conversion table in the USDA Technical Procedures Manual for this conversion. Use of equation (1) results in a difference of less than 0.1% in the Brix conversions and sugar calculations compared to the previous versions.
Back to topSpecific Gravity <--> Oechsle
Oechsle is a scale of must weight and is used mainly in Germany for the Prädikat classification of wines. There are two definitions of Oechsle currently in use. The first is based on specific gravity, and is referred to as "old" Oechsle in Germany. It is still used in Luxemburg and Switzerland. This Oechsle scale is calculated as:
Oeo = 1000(sg - 1.0) (2)
where
Oeo = degrees Oechsle (old)
sg = specific gravity
The new Oechsle scale is based on refractive index, and is the current official Oechsle scale in Germany. This scale is based on the following relationship with refractive index, and has a range of validity from 40° to 120° Oechsle (Schmitt, 1983 and Jakob, 1995):
Oen = 2639.22ri - 3514.83 (3)
where
Oen = degrees Oechsle (new)
ri = refractive index
FermCalc uses equations (1) and (37) to convert between SG and refractive index in order to calculate Oechsle from equation (3). Outside of the range of validity of equation (3), values of Oen are linearly interpolated between the Oen values at the limits of the valid range and Oeo based on equation (2) at the minimum and maximum values of sg.
Back to topSpecific Gravity <--> Baumé
The Baumé hydrometer scale was devised by French chemist Antoine Baumé and is still used in the food and chemical industries. There are two Baumé scales: one for liquids heavier than water, and one for liquids lighter than water. For liquids that are heavier than water, 0°Bé corresponds to the reading for pure water, and 15°Bé corresponds to the reading of a solution of 15% NaCl by mass. For liquids that are lighter than water, 10°Bé marks the level for pure water and 0°Bé corresponds to a solution that is 10% NaCl by mass.
Note that the heavy and light scales go in opposite directions.
The equation for liquids heavier than water is:
Bé = 145 - 145/sg (4)
where Bé is degrees Baumé.
The equation for liquids lighter than water is:
Bé = 140/sg - 130 (5)
Only the scale for liquids heavier than water is included in FermCalc because this is the only one used in winemaking.
Back to topSpecific Gravity <--> Klosterneuburger Mostwaage (KMW)
The Klosterneuburger Mostwaage (KMW) scale is used in Austria as a measure of the sugar content of a must. It is used to categorize wines into the various Austrian quality classifications. It is known as the Babo scale in Italy. It is legally related to the old Oechsle scale as follows:
Oeold = 0.022·KMW2 + 4.54·KMW (7)
where KMW is degrees KMW. FermCalc converts between KMW and sg by direct solution of equations (2) and (7).
Back to topSpecific Gravity <--> Twaddell
The Twaddell scale is an SG scale for liquids heavier than water that is used mainly in the United Kingdom. The conversion to SG is similar to that for the Oechsle scale above, but it uses a factor of 200 instead of 1000, or:
Tw = 200(sg - 1.0) (6)
where Tw is degrees Twaddell.
Back to topSpecific Gravity <--> Density
The SG of a substance is the ratio of its density at 20ºC to the density of water at 20ºC. To convert SG to density we simply need to multiply the SG by the density of water and by the appropriate conversion factor. The conversion factors used in FermCalc are:
grams/liter = 1000·sg·ρw (8) kilograms/liter = 1.0·sg·ρw (9) kilograms/cubic meter = 1000·sg·ρw (10) pounds/gallon (US) = 8.34540445·sg·ρw (11) pounds/gallon (Imperial) = 10.02241726·sg·ρw (12) pounds/cubic feet = 62.42796058·sg·ρw (13)
where:
sg = specific gravityBack to top
ρw = density of water = 0.9982 kg/liter at 20ºC
Specific Gravity <--> g/L Sugar
Sugar content in grams/liter (g/L) is not really an SG unit, but it's included here because it's a useful quantity for a number of calculations. It's important to note here that this conversion is only strictly valid for pure aqueous sucrose solutions, so it cannot be used for any liquids that contain alcohol. Also, it should not be confused with the density units of grams/liter. The equation to determine g/L sugar from sg is:
g/L Sugar = 10·sg·B·ρw (14)
Calculating sg from g/L Sugar requires an iterative calculation since B is a function of sg.
Back to topSpecific Gravity <--> Potential Alcohol
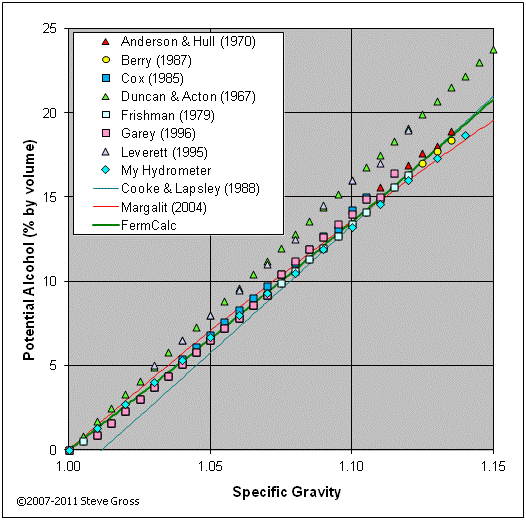
While potential alcohol is not really an SG unit, this conversion is often used by winemakers to relate the initial sugar content of a must to the potential alcoholic content of the finished wine. For this calculation FermCalc uses the method proposed by Duncan and Acton (1967), which requires measurement of both the initial and final specific gravities. For the purpose of this calculation, which is generally used to establish the initial sgi of a must, FermCalc assumes the final SG sgf is 1.0. The equations are as follows in terms of sg:
ap = 1000(sgi - sgf)/F (15) F = 7.75 - 3000(sgc - 1.0)/800 (16) sgc = sgi - 0.007 (17)
where
ap = potential alcohol, % by volume
sgi = initial specific gravity
sgf = final specific gravity
F = conversion factor
sgc = initial specific gravity corrected for non-sugar solutes
Combining equations (15) through (17) above and assuming that sgf equals 1.0 yields the following equation.
ap = 1000(sgi - 1.0)/[7.75 - 3.75(sgi - 1.007)] (18)
The calculated potential alcohol values are constrained to a maximum of 100% and a minimum of 0%.
The graph below compares potential alcohol tables from various sources to equation (18) above. The FermCalc results agree well with the lower trend. The higher trend of points (from Duncan & Acton, 1967 and Leverett, 1995) presumably do not account for non-sugar solutes (dissolved solids which increase the SG but are not converted to alcohol during fermentation).
Acidity Conversions
Acid Reference Conversions
When we titrate a must or wine for acidity, all we really determine is the number of available hydrogen (H+) ions in the wine and not the types of acid present. For this reason we must choose an acid as a reference in order to express the acidity as a concentration.
Different winemaking texts use different acid references when referring to titratable acidity levels. Most use tartaric acid as the reference, with units of either percent or grams/liter (parts per thousand, or ppt). However, other texts use different acids as the reference, with sulfuric acid being a popular alternative to tartaric acid.
To develop the conversion factors that convert from one acid reference to the other we need to know their molecular weights and the number of H+ ions each molecule of the acid contributes to make the solution acidic. The table below lists these values for the most common acid references, compiled from Margalit (2004) and Weast (1977).
| Acid | Molecular Weight | H+ Ions |
|---|---|---|
| Tartaric | 150.09 | 2 |
| Malic | 134.09 | 2 |
| Citric | 192.12 | 3 |
| Lactic | 90.08 | 1 |
| Acetic | 60.05 | 1 |
| Sulfuric | 98.08 | 2 |
The number of moles of H+ ions an acid contributes can be calculated as:
M = i(m/mw) (19)
where
M = moles of H+ ions
i = number of H+ ions per molecule
m = mass of acid, grams
mw = molecular weight of acid, grams/mole
The mass of the acid in solution is simply the acidity multiplied by the volume, or:
m = a·v (20)
where
v = volume of solution, liters
a = acidity, grams/liter
Combining equations (18) and (19) we get:
M = i(a·v/mw) (21)
To convert from one acid reference to the other, we know that the number of moles of H+ ions and the volume are the same no matter what reference we use, so we can write:
i1(a1/mw1) = i2(a2/mw2) (22)
Rearranging equation (22) to convert from on acid reference to another we get:
a2 = a1(i1/i2)(mw2/mw1) (23)
For example, to convert from 0.420% sulfuric to % tartaric:
(0.420% sulfuric)·(2/2)·(150.09/98.08) = 0.643% tartaricBack to top
Grams/Liter <--> Percent Conversions
This is a simple conversion. Since grams/liter is parts per thousand (ppt), and percent is parts per hundred, we simply need to divide grams/liter by 10 to get percent, or:
percent = grams/liter / 10 (24)
Grams/Liter <--> mEq/L Conversions
An milli-equivalent (mEq) is the amount of a substance that will react with or supply one-thousandth of a mole of hydrogen ions (H+) in an acid-base reaction. If we know the mass of an acid in solution, we can calculate the mEq/L as:
mEq/L = 1000·i(m/mw)/v (25)
Substituting equation (20) into equation (25) we get:
Back to top
mEq/L = 1000·i·a/mw (26)
Alcohol Content Conversions
Below are details of the alcohol content unit conversions. All alcohol content values are converted to % alcohol by volume when they are entered, and are subjected to an upper limit of 100% and a lower limit of 0%.
Back to top% Alcohol by Volume <--> % Alcohol by Weight
The percentages of alcohol by weight and alcohol by volume for a water/alcohol mixture are defined respectively as:
aw = 100(ma/mm) (27) av = 100(va/vm) (28)
where
aw = alcohol content, % by weight
ma = mass of alcohol, kg
mm = mass of the water/alcohol mixture, kg
av = alcohol content, % by volume
va = volume of the alcohol, liters
vm = volume of the water/alcohol mixture, liters
We can relate the volumes and the masses of the alcohol and the mixture as:
ma = vaρa (29) mm = vmρm (30)
where
ρa = density of alcohol, kg/liter
ρm = density of the water/alcohol mixture, kg/liter
Substituting equations (29) and (30) into equation (27) we get:
aw = 100(va/vm)(ρa/ρm) (31)
Then we can substitute equation (28) into equation (31) to get:
aw = av(ρa/ρm) (31)
Re-arranging equation (32) we get:
av = aw(ρm/ρa) (33)
FermCalc uses the general formula for calculating the densities of mixtures of ethanol and water found in International Recommendation 22: International Alcoholometric Tables by the International Organisation of Legal Metrology (OIML, 1973) to calculate the densities of alcohol ρa and water/alcohol mixtures ρm at 20ºC that are required to perform the conversion. When performing the conversion for a wine with a specified SG, the actual wine density is used in place of ρm in equation (33).
Back to top% Alcohol by Volume <--> Proof (US)
The Proof scale in the United States is simply equal to twice the % alcohol by volume, or:
Pu = 2.0av (34)
where
Pu = Proof (US)Back to top
av = alcohol content, % by volume
% Alcohol by Volume <--> Proof (British)
The term "proof" probably originated from test of alcoholic strength in which the spirit was mixed with gunpowder and ignited (Schidrowitz, 1911). If the gunpowder didn't burn, the spirit was deemed to be "under proof". According to the Alcoholic Liquor Duties Act (1979), "Spirits shall be deemed to be at proof if the volume of the ethyl alcohol contained therein made up to the volume of the spirits with distilled water has a weight equal to that of twelve-thirteenths of a volume of distilled water equal to the volume of the spirits, the volume of each liquid being computed as at 51ºF." Using the OIML formula, we can calculate the density of water at 51ºF as 999.64 kg/m3, twelve-thirteenths of which is 922.74 kg/m3, which equates to an alcohol content of 57.15% by volume. The conversion then becomes:
Pb = av / 0.5715 (35)
where
Pb = Proof (British)Back to top
av = alcohol content, % by volume
Concentration Conversions
All concentrations in FermCalc are expressed in terms of mass of substance per unit volume of solution. Converting from one set of units to another is a simple matter of converting the mass units in the numerator and the volume units in the denominator. For example, to convert from g/mL to lb/gal we can write:
(1 g) (1 lb / 453.59 g) / [(1 mL) ( 1 gal / 3785.4 mL)] = 8.3454 lb/gal (36)
Concentrations expressed as mass per unit mass - such as percent, parts per thousand (ppt), and parts per million (ppm) - are often used interchangeably with their mass per unit volume counterparts. These mass/mass units are shown in parentheses next to the mass/volume units. Strictly speaking, these equivalencies are only accurate if the SG of the solution is equal to 1.0. Fortunately most of the solutions we deal with in winemaking have specific gravities close to 1.0.
Back to topRefractivity Conversions
Refractivity conversions are included mainly to allow the use of refractometers with a variety of different scales to be used for the calculation of alcohol content described here. These conversions are only valid for refractometers calibrated for aqueous sucrose solutions at 20°C.
Refractive Index <--> Refractometer Brix
In order to convert between refractive index and refractometer Brix, FermCalc uses the equation published in the Sugar Journal (1970), which was derived from the work of Rosenhauer, Schneider and Emmerich (1966) for the International Commission for Uniform Methods of Sugar Analysis (ICUMSA), and serves as the basis for the AOAC refractive index tables (Williams, 1984). The equation is:
B = 0.0087 + 699.82353(ri - 1.3330) - 1801.9215(ri - 1.3330)2
+ 4696.422(ri - 1.3330)3 - 6427.26(ri - 1.3330)4(37)
where
B = degrees Brix
ri = index of refraction
In order to convert from Brix to refractive index, FermCalc uses an iterative technique to solve equation (37) for ri.
The result of equation (37) is adjusted for small values of B so that it equals 0 at an ri value of 1.333.
Refractive Index <--> Oechsle
FermCalc converts between Oechsle (old) and refractive index by combining the conversions in equations (1), (2), and (37). FermCalc converts between Oechsle (new) and refractive index using equation (3) inside its range of validity from 40 to 120 °Oe, and extrapolates to other values as described above.
Refractive Index <--> Baumé
FermCalc converts between Baumé and refractive index by combining the conversions in equations (1), (4), and (37).
Refractive Index <--> KMW
FermCalc converts between KMW and refractive index by combining the conversions in equations (1), (2), (7), and (37).Refractive Index <--> Zeiss Units
The Zeiss refractivity scale was originally used on older Zeiss immersion refractometers and is still used today on some handheld refractometers. This scale ranges from -5 to 105, corresponding to refractivity index values of 1.32539 to 1.36640 (Thurston, 1922). Thee upper end of the scale corresponds to a Brix value of 21.53, so it has limited applicability for winemaking.
FermCalc converts between Zeiss units and refractive index using the equation adopted by the AOAC (Williams, 1984):
ri = 1.327338 + 3.9347·10-4Zeiss - 2.0446·10-7Zeiss2 (38)
where
ri = index of refractionBack to top
Zeiss = Zeiss units
© 2007-2021 Steve Gross
Last updated
11 September 2021.