Chaptalization & Dilution Calculator

Introduction

The Chaptalization & Dilution Calculator determines the amounts of sweetener and/or water to add to a given must to achieve a target specific gravity (SG) and volume.  Alternatively, the resulting SG and volume can be calculated from the specified sweetener and water additions.  The sweetener can be either sugar, honey, or concentrate.

FermCalc offers three options for this calculation:

1. Specify Target SG  >  Calculate H2O/Sugar Additions and Volume – Specify the target SG, the initial SG, and the initial volume, and FermCalc will calculate the required additions of water or sweetener as well as the resulting volume after the addition.
2. Specify Target SG and Volume  >  Calculate H2O/Sugar Additions – Specify the target SG, the initial SG, the target volume, and the initial volume, and FermCalc will calculate the required additions of water and/or sweetener to achieve both targets.
3. Specify H2O/Sugar Additions  >  Calculate Resulting SG and Volume – Specify the initial SG, the initial volume, and the amounts of water and/or sugar to be added, and FermCalc will calculate the resulting volume and SG.

If the second calculation option is selected and you get a message that says “Target Volume must be increased or Initial Volume must be reduced.”, your target volume is too small to allow the additions that are required to achieve the target specific gravity. In this case, change back to the first calculation option to calculate the minimum target volume required to achieve the desired specific gravity.

The honey and concentrate calculations are very similar. The main difference is that honey additions are specified in mass units, and concentrate additions are specified in volume units.

Input Field Definitions

Sweetener – The type of sweetener to be added, either sugar, honey, or concentrate.  The SG of the sweetener must be specified if honey or concentrate is selected.

Target SG – The desired SG (20°C/20°C) of the must after chaptalization or dilution.  Required only if either the first or second calculation option is selected.  Range: 0.77193 to 1.55454

Initial SG – The SG (20°C/20°C) of the must prior to chaptalization or dilution.  Range: 0.77193 to 1.55454

Target Volume – The desired volume of the must after chaptalization or dilution.  Required only if the second calculation option is selected.

Initial Volume – The volume of the must prior to chaptalization or dilution.  Required only if either the first or third calculation option is selected.

Sugar (or Honey or Concentrate) Added – The amount of sweetener added to the must.  Required only if the third calculation option is selected.

Water Added – The amount of water added to the must.  Required only if the third calculation option is selected.

Output Field Definitions

Sugar (or Honey or Concentrate) Required – The calculated amount of sweetener required to yield the desired specific gravity and volume.  Reported only if either the first or second calculation option is selected.

Water Required – The calculated amount of water required to yield the desired specific gravity and volume.  Reported only if either the first or second calculation option is selected.

Resulting SG – The SG (20°C/20°C) of the must after adding the specified amounts of sweetener and water.  Reported only if the third calculation option is selected.

Resulting Volume – The calculated volume of the must after adding the specified amounts of sweetener and water.  Reported only if the third calculation option is selected.

Back to top

Calculation Details

All of the chaptalization and dilution calculations are based on the previously developed mass balance equations (2-12) and (2-13). They’ll just be re-arranged and solved differently depending on what we’re solving for. These equations are repeated below for completeness.

vfsgfρwBf = visgiρwBi + msaBs	(2-12)
vfsgfρw = visgiρw + msa + vwaρw	(2-13)

where:

v_i = initial must volume, liters

v_f = final volume, liters

sg_i = initial specific gravity

sg_f = final specific gravity

B_i = initial Brix

B_f = final Brix

B_s = sugar Brix

ρ_w = density of water = 0.9982 kg/liter at 20ºC

m_sa = mass of sugar added, kg

v_wa = volume of water added, liters

Option 1: Specify Target SG  >  Calculate H2O/Sugar Additions and Volume

In this case the known values are v_i, sg_i, and sg_f.

If the target gravity is greater than the initial gravity, we know we’ll be adding a sweetener and no water, so equation (2-13) reduces to:

vfsgfρw = visgiρw + msa

(2-14)

Substituting the right-hand side of equation (2-14) into equation (2-12) we get:

(visgiρw  + msa)Bf = visgiρwBi  + msaBs

(2-15)

Then we can re-arrange equation (2-15) to solve for the amount of sweetener to add:

msa = visgiρw(Bf – Bi) / (Bs – Bf)

(2-16)

Knowing how much sweetener we’re adding we can then re-arrange equation (2-14) to solve for the final volume after the addition of the sweetener, which gives us:

vf = (visgiρw + msa) / (sgfρw)

(2-17)

The graphs below validate equations (2-16) and (2-17) by comparing their results to tabular data from various sources and to the results of my own experiments.

Back to top

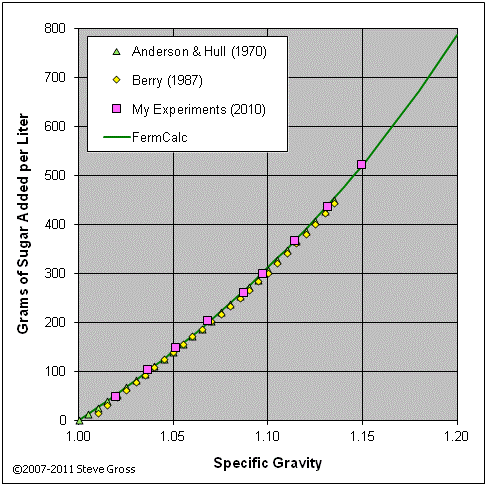
If the target gravity is less than the initial gravity, we know we’ll need to add water to reduce the gravity. Since we know we’ll be adding water only and no sugar, equation (2-12) reduces to:

vfsgfρwBf = visgiρwBi

(2-18)

Now we can solve equation (2-18) for the final volume:

vf = (visgiBi) / (sgfBf)

(2-19)

Since we know we’ll only be adding water to the mixture, equation (2-13) reduces to:

vfsgfρw = visgiρw + vwaρw

(2-20)

Solving equation (2-20) for the volume of water to add we get:

vwa = vfsgf – visgi

(2-21)

Back to top

Option 2: Specify Target SG and Volume  >  Calculate H2O/Sugar Additions

In this case the known values are v_i, v_f, sg_i, and sg_f. To calculate the amount of sugar to add, we simply need to re-arrange equation (2-12) and solve for the amount of sweetener to add, or:

msa = (vfsgf ρwBf – visgiρwBi) / Bs

(2-22)

Knowing the amount of sweetener to add we can then re-arrange equation (2-13) to solve for the amount of water to add:

vwa = (vfsgfρw – visgiρw – msa) / ρw

(2-23)

The graph below validates equation (2-22) by comparing its results to tabular data from various sources and to the results of my own experiments.

Back to top

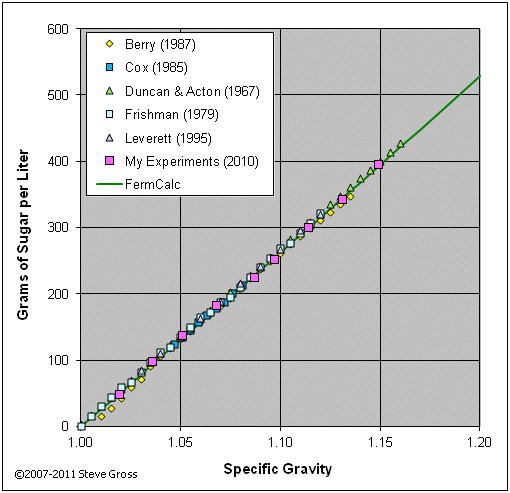
Option 3: Specify H2O/Sugar Additions  >  Calculate Resulting SG and Volume

In this case the known values are v_i, sg_i, m_sa, and m_wa. To calculate the resulting specific gravity sg_f we first substitute the right-hand side of equation (2-13) into equation (2-12) to get:

(visgiρw + msa + vwaρw)Bf = visgiρwBi + msaBs

(2-24)

Then solving for B_f we get:

Bf = (visgiρwBi + msaBs) / (visgiρw + msa + vwaρw)

(2-25)

Knowing B_f we can then determine sg_f from the Brix conversion equation.

After we determine sg_f we can solve equation (2-13) for v_f to get:

vf = (visgiρw + msa + vwaρw) / (sgfρw)

(2-26)

Back to top