Introduction
Port wine is traditionally made by adding a fortifier to a fermenting grape must at a specific point during the fermentation. The addition of the fortifier stops the fermentation by elevating the alcohol content of the must above the alcohol tolerance ot the yeast, thereby leaving the desired amount of residual sugar. The fortifier is traditionally a distilled wine spirit, known as aguardente or brandy, with an alcohol content of 76-78% v/v.
The Fortification Point Calculator determines 1) the specific gravity (SG) at which to stop an active fermentation to yield the desired level of residual sugar in a fortified wine, and 2) the amount of fortifier required yield the desired alcohol level. It accounts for the alcohol produced during fermentation, and for the dilution of the residual sugar by the addition of the fortifier.
After this “ideal” fortification point is calculated, the user has the option to override the calculated value of SG at the fortification point in order to model the impact of fortifying at a different SG. If the entered SG is lower than the ideal value, then there is not enough residual sugar to achieve the target sugar content, so the sweetener addition required to achieve the target sugar content is calculated. If the entered SG is higher than the ideal value, the sugar content will exceed the target sugar content after fortification, so the resulting sugar content after the addition of fortifier is calculated.
All volumes and specific gravities have a temperature basis of 20°C (68°F). It is assumed that the fortifier contains only ethanol and water, and that the sweetener contains only sucrose and water.
Input Field Definitions
Sweetener – The type of sweetener to be added, either sugar, honey, or concentrate. The SG of the sweetener must be specified if honey or concentrate is selected. This is only used if the user enters a value of wine SG at fortification that is less than the “ideal” value, in which case the addition of a sweetener is required to achieve the target sugar content.
Fortifier Alcohol Content – The alcohol content of the fortifier being added.
Wine Volume – The volume of the fermenting wine at the time of fortification. If this volume option is selected, the resulting volume after fortification is calculated.
Target Volume – The volume of the fortified wine after the addition of the calculated fortifier and sweetener additions. If this volume option is selected, the required wine volume at the fortification point is calculated.
Initial Must SG – The SG of the must prior to the start of fermentation.
Target Alcohol Content – The desired alcohol content of the fortified wine.
Target Sugar Content – The desired total solids content of the fortified wine after the addition of fortifier and sweetener.
Wine SG at Fortification – The SG of the fermenting wine at the time of fortification. This field can serve either as an input field or an output field. Initially the “ideal” fortification point SG is calculated based on the inputs above. If the calculated value is overridden by the user, then either the target sugar content or the required sweetener addition are calculated, depending on whether the entered SG value is greater than or less than the ideal value.
Output Field Definitions
Wine Alcohol Content – The calculated alcohol content of the fermenting wine at the fortification point.
Wine Sugar Content – The calculated total solids content (true Brix) of the fermenting wine at the fortification point.
Wine Required – The volume of fermenting wine required to yield the desired alcohol content, sugar content, and volume. Reported only if target volume is selected as the volume option above.
Fortifier Required – The calculated amount of fortifier required to yield the desired alcohol content, sugar content, and volume.
Sugar (or Honey or Concentrate) Required – The calculated amount of sweetener required to yield the desired alcohol content, sugar content, and volume. This will be zero unless the user enters a wine SG at fortification that is less than the “ideal” value.
Resulting Volume – The calculated volume of the fortified wine after adding the specified amounts of fortifier and sweetener. Reported only if wine volume is selected as the volume option above.
Calculation Details
The fortification point calculations are based mainly on the previously developed mass balance equations (7-16), (7-17), and (7-18), repeated here for completeness:
vfsgfρwBf = visgiρwBi + msaBs |
(7-16) |
vfsgfρwawf = visgiρwawi + vfasgfaρwawfa |
(7-17) |
vfsgfρw = visgiρw + vfasgfaρw + msa |
(7-18) |
where:
vi = initial must volume, liters
vf = final volume, liters
sgi = initial specific gravity
sgf = final specific gravity
Bi = initial Brix
Bf = final Brix
Bs = sugar Brix
awi = wine initial alcohol level, % by weight
awf = final alcohol level, % by weight
awfa = fortifier alcohol level, % by weight
ρw = density of water = 0.9982 kg/liter at 20ºC
msa = mass of sugar added, kg
vwa = volume of water added, liters
We’ll need to specify the initial specific gravity of the must sgm in order to calculate the alcohol produced during the fermentation from the drop in specific gravity. We’ll use the Balling Method to calculate the amount of alcohol produced because it’s simple to apply and seems to be just as accurate as the other SG-drop methods.
In this case the known values are vi (or vf), sgm, awf, Bf, sgf, sgfa, awfa, and msa. Since we’re not adding a sweetener in this case we can eliminate the terms msa and Bs. We need to solve for vf (or vi), sgi, awi, Bi, and vfa. Since sgi, awi, and Bi are all interdependent, we’ll need to iterate to find a solution.
We start by substituting equation (7-18) into equation (7-17) to eliminate vfa and solve for vf:
vf = [visgi(awfa – awi)] / [sgf(awfa – awf)] |
(7-26) |
Or, if we’re solving for vi:
vi = [vfsgf(awfa – awf)] / [sgi(awfa – awi)] |
(7-27) |
In these equations the subscript i denotes values at the fortification point. For the first iteration we’ll assume a value of 1.0 for sgi. After solving equation (7-26) or (7-27) we can solve equation (7-16) for Bi:
Bi = vfsgfBf / visgi |
(7-28) |
Next we update the estimate of sgi using Hackbarth model with the calculated values of Bi and awi, and then repeat the calculations in equations (7-26) through (7-28) until we converge on a solution. Then we can solve equation (7-18) for the volume of fortifier to add:
vfa = (vfsgf – visgi) / (sgfa) |
(7-29) |
After the “ideal” fortification point is calculated, the user has the option to override the calculated value of sgi in order to model the impact of fortifying at a different SG. When this is done, we first calculate the resulting value of awi using the Balling method and the value of Bi using the Hackbarth model.
If the value of sgi entered by the user is lower than the ideal value, then there is not enough residual sugar to achieve the target sugar content. In this case we can then solve equation (7-19) or (7-22) above, depending on whether the initial volume or the target volume were specified, and then solve equations (7-20) and (7-21) to determine the required additions of fortifier and sugar.
If the value of sgi entered by the user is higher than the “ideal” fortification point, then the sugar content of the wine will be too high to yield the target sugar content. In this case, no sweetener will be added and we’ll need to calculate the resulting sugar content Bf. To do this we’ll follow an iterative procedure similar to the one described above utilizing equations (7-26) through (7-29), but we’ll use a starting value of 1.0 for sgf, and instead of equation (7-28) we’ll solve equation (7-16) for Bf:
Bf = visgiBi / vfsgf |
(7-30) |
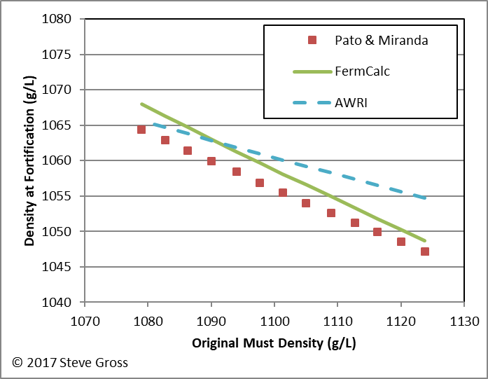
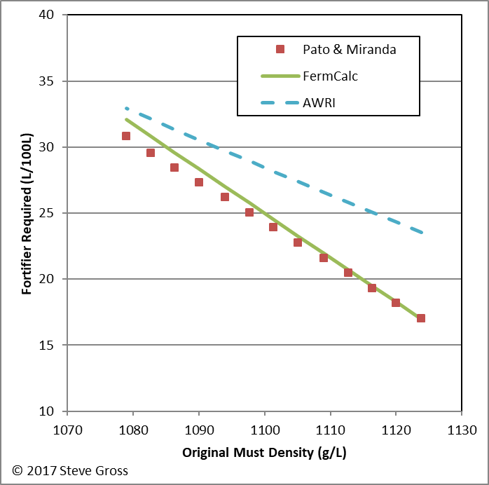
Below the results of the FermCalc Fortification Point calculator are compared to the classic work of Pato & Miranda (1938) and to the fortification calculator found on the Australian Wine Research Institute (AWRI) web site. The density at fortification and the amount of fortifier to add were calculated to yield a fortified wine with an alcohol content of 20% v/v and a density of 1028.51 g/L using a fortifying spirit with an alcohol content of 77% v/v. The FermCalc results generally fall between the two other methods, and show better agreeement with the Pato & Miranda results. (The forumulas used by the AWRI calculator aren’t documented on their site, but it apparently uses the same formulas found on the Monash Scientific site because they give identical results.)